All About Linked Lists 🎩¶

In Chapter 5 we carefully examined Python’s array-based list class, and in Chapter 6 we demonstrated use of that class in implementing the classic stack, queue, and dequeue ADTs.

Python’s list class is highly optimized, and often a great choice for storage. With that said, there are some notable disadvantages:

The length of a dynamic array might be longer than the actual number of elements that it stores.
Amortized bounds for operations may be unacceptable in real-time systems.
Insertions and deletions at interior positions of an array are expensive.

In this chapter, we introduce a data structure known as a linked list, which provides an alternative to an array-based sequence (such as a Python list).

Both array-based sequences and linked lists keep elements in a certain order, but using a very different style.

An array provides the more centralized representation, with one large chunk of memory capable of accommodating references to many elements.

A linked list, in contrast, relies on a more distributed representation in which a lightweight object, known as a Node, is allocated for each element.

Each node maintains a reference to it's element and one or more references to neighboring nodes in order to collectively represent the linear order of the sequence.

train — Linked List is just like a Train!

We will demonstrate a trade-off of advantages and disadvantages when contrasting array-based sequences and linked lists.

Elements of a linked list cannot be efficiently accessed by a numeric index k, and we cannot tell just by examining a node if it is the second, fifth, or twentieth node in the list.

However, linked lists avoid the three disadvantages noted above for array-based sequences.

Where ?¶

You might be wondering — where is a linked list useful?

A Use/Example of Linked List (Doubly) can be Lift in the Building.

A person have to go through all the floor to reach top (tail in terms of linked list).
A person can never go to some random floor directly (have to go through intermediate floors/Nodes).
A person can never go beyond the top floor (next to the tail node is assigned None).
A person can never go beyond the ground/last floor (previous to the head node is assigned None in linked list).

Insertion and deletion within the sequence in \(O(1)\) time, compared to arrays, this is great!

Singly Linked Lists¶

Let's start really small 🥰

Summary: We have head and size. Node is within the class. If there is a tail, check the edge cases.

A Singly Linked List (SLL), in its simplest form, is a collection of nodes that collectively form a linear sequence.

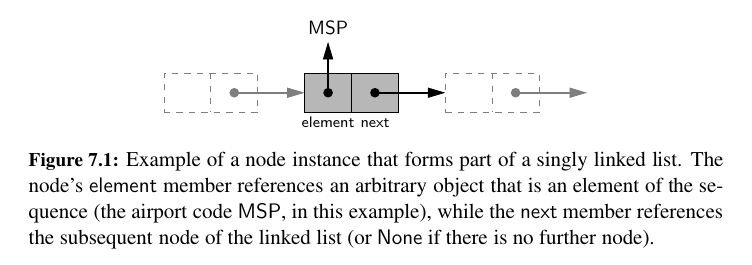
Each node stores a reference to an object that is an element of the sequence, as well as a reference to the next node of the list:

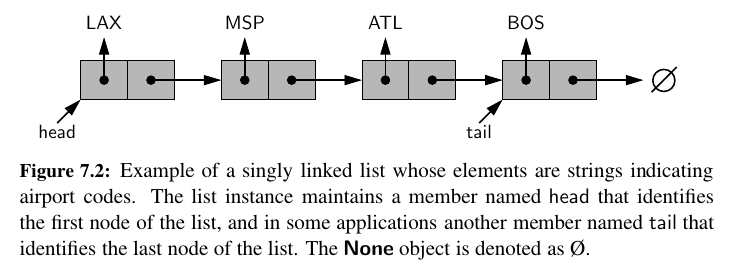
airport_linked_list — A real example of a Linked List

The first and last node of a linked list are known as the head and tail of the list, respectively.

Head identifies first node, tail identifies last node. 💕

By starting at the head, and moving from one node to another by following each node’s next reference, we can reach the tail of the list.

We can identify the tail as the node having None as its next reference.

This process is commonly known as traversing the linked list.

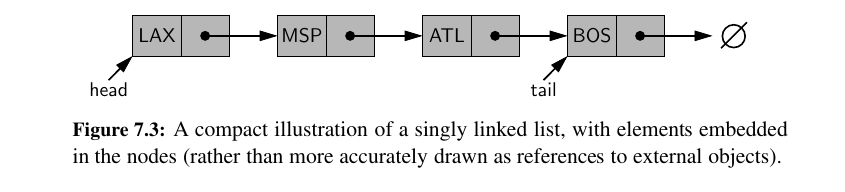
For the remainder of this chapter, we continue to illustrate nodes as objects, and each node’s “next” reference as a pointer.

However, for the sake of simplicity, we illustrate a node’s element embedded directly within the node structure, even though the element is, in fact, an independent object.

compact_showing_for_linked_list — A compact view of a Linked List

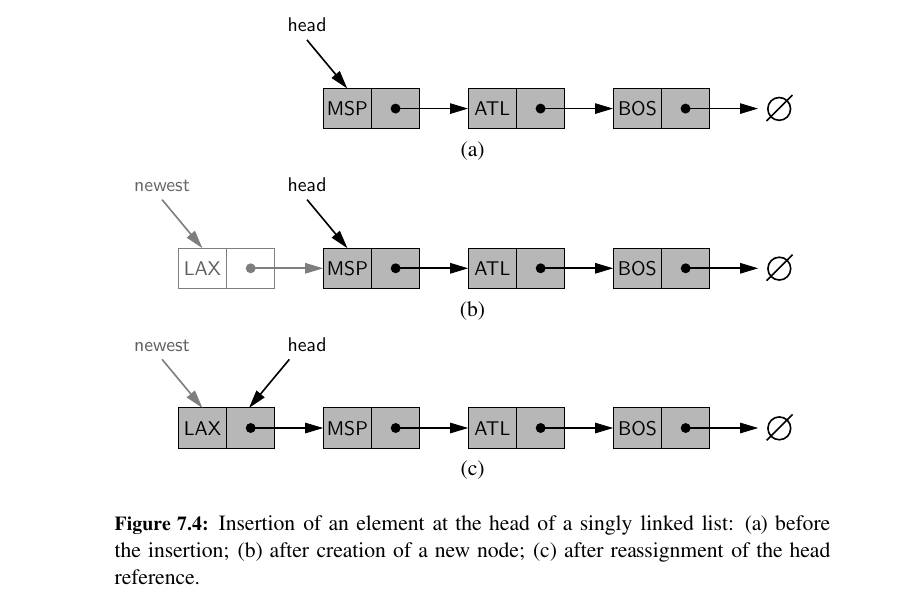
Inserting an Element at the Head of a Singly Linked List¶

There is no fixed size in a linked list, so it uses space proportionally to its current number of elements.

How do we add an element to head?

- Make a new node
- Make it point to head
- Make head point to the new node (new head)
- increment size

insertion_at_head — Insertion at head for a SLL

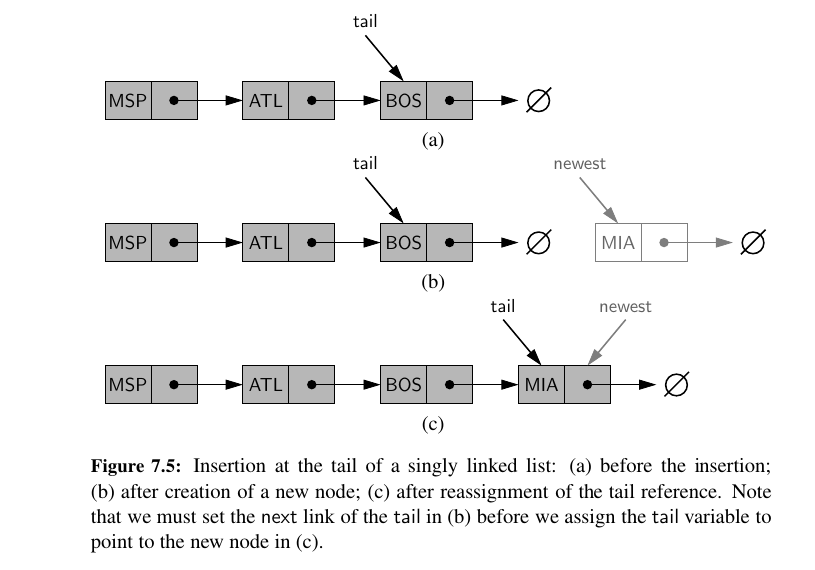
Inserting an Element at the Tail of a Singly Linked List¶

How do we add an element to the tail?

- Make a new node with no next
- Make tail point to the new node (new tail)
- Increment size

insertion_at_TAIL — Insertion at tail for a SLL

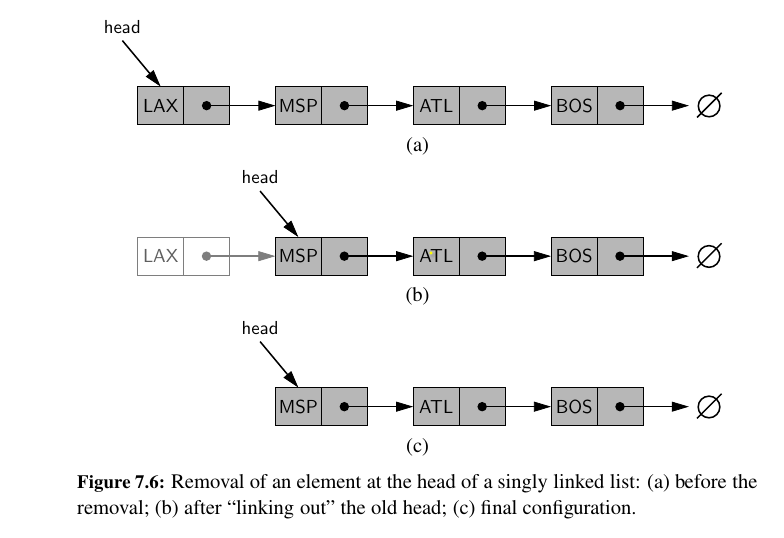
Removing an Element from a Singly Linked List - Head¶

How do we remove an element from head ?

- Make head point to current head.next
- delete Node (Auto GC)
- decrement size

This is essentially the reverse operation of inserting a new element to the head. 😌

removal_from_sll — Remove an element from a SLL

Removing an Element from a Singly Linked List - Tail 🎃¶

Unfortunately, we cannot easily delete the last node of a singly linked list.

Even if we maintain a tail reference directly to the last node of the list, we must be able to access the node before the last node in order to remove the last node.

But we cannot reach the node before the tail by following next links from the tail.

The only way to access this node is to start from the head of the list and search all the way through the list (We have to traverse it all!).

But such a sequence of link-hopping operations could take a long time.

If we want to support such an operation efficiently, we will need to make our list doubly linked 😍

Linked Lists in Real World 🤨¶

In an interview if you see a question about Linked Lists, you will probably be given the most simple ListNode class like the one down below:

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

Using this node in a LinkedList you can solve the question you are given.

If you are not given such class, you can write it yourself. Because these are the most basic definitions for a LinkedList.

If you are ever asked to implement a stack or a queue with Linked Lists, you now what to do.

You know that for a single linked list, you can insert and remove from the head in \(O(1)\) which would be applicable for stacks.

You also know that you can insert from tail but remove from head, so for a queue, adding elements from tail and removing from head would be smarter.

Here is an example of implementing a MinStack with Linked lists:

min_stack_with_linked_list.py
class Node:
    def __init__(self, value, min_val, next = None):
        self.value = value
        self.min_val = min_val
        self.next = next

class MinStack:
    """A minimum element special stack implemented with LLs"""
    def __init__(self):
        self.head = None

    def push(self, val):
        """Push the element onto stack, update min value"""
        if not self.head:
            # a new LL is forming. Head is val.
            new_node = Node(val, val)
        else:
            new_min = min(self.head.min_val , val)
            new_node = Node(val, new_min, self.head)
        self.head = new_node

    def pop(self):
        """Pop the element on top of stack
        Not returning the answer"""
        if self.head:
            self.head = self.head.next

    def top(self):
        if self.head:
            return self.head.value

    def getMin(self):
        if self.head:
            return self.head.min_val

# Input
# ["MinStack","push","push","push","getMin","pop","top","getMin"]
# [[],[-2],[0],[-3],[],[],[],[]]
# Output 
# [null,null,null,null,-3,null,0,-2]

Implementing a Stack with a Singly Linked List¶

This part is just for practice.

In designing such an implementation, we need to decide whether to model the top of the stack at the head or at the tail of the list. Where should the head be?

We learned that we can efficiently add and remove from the head, so top of the stack should be the Linked List head!

Because that is what we do in a stack. We insert at top, we remove from top. That is it!

There is clearly a best choice here; we can efficiently insert and delete elements in constant time only at the head. Since all stack operations affect the top, we orient the top of the stack at the head of our list.

Here is the code:

stack_with_linked_list.py
class LinkedStack:
    """LIFO Stack implementation using a singly linked list for its storage"""

    class _Node:
        "Lightweight, nonpublic class for storing a singly linked list node"
        __slots__ = "_element", "_next"  # streamline memory usage

        def __init__(self, element, next): # initialize node's fields
            self._element = element # user's element
            self._next = next # reference to next node

    def __init__(self):
        """Make an empty stack"""
        self._head = None # reference to head Node
        self._size = 0 # initial size

    def __len__(self):
        """Return the number of elements in the Stack"""
        return self._size

    def is_empty(self):
        """Return True if stack is empty"""
        return self._size == 0

    def push(self,e):
        """Add element e to the top of the stack"""
        self._head = self._Node(e, self._head) # Make a new node and link it to head
        self._size += 1

    def top(self):
        """Return but do not remove the top element from the stack"""
        if self.is_empty(self):
            raise Exception("Stack is empty")
        return self._head._element

    def pop(self):
        """Remove the top element from the stack and return it"""
        if self.is_empty(self):
            raise Exception("Stack is empty, nothing to pop")
        answer = self._head._element # we gotta return this
        # new head is next
        self._head = self._head._next # head now should be pointing to the next node
        # decrement size
        self._size -= 1
        return answer

Here is the analysis of our operations:

Method	Running Time
`S.push(e)`	\(O(1)\)
`S.pop()`	\(O(1)\)
`S.top()`	\(O(1)\)
`len(S)`	\(O(1)\)
`S.is_empty()`	\(O(1)\)

All bounds are worst case and space usage is \(O(n)\) where n is the current number of elements in the stack.

Implementing a Queue with a Singly Linked List¶

This is also just for practice.

What does a queue do? It adds elements, enqueues them from the back and pop or remove or dequeue them from the front.

So clearly, we need to set our linked Lists so that the head is the front of the queue, and back is the end of the queue. We can enqueue in constant time in the queue, we can dequeue from front in constant time as well.

The natural orientation for a queue is to align the front of the queue with the head of the list, and the back of the queue with the tail of the list, because we must be able to enqueue elements at the back, and dequeue them from the front.

Here is the code:

queue_with_linked_list.py
class LinkedQueue:
    """FIFO queue implementation using a singly linked list for storage."""

    class _Node:
        """Lightweight, nonpublic class for storing a singly linked node."""
        __slots__ = "_element",  "_next" # streamline memory usage

        def __init__(self, element, next):
            self._element = element # reference to user element
            self._next = next # reference to next node

    def __init__(self):
        """Create an empty queue."""
        self._head = None
        self._tail = None
        self._size = 0 # number of queue elements

    def __len__(self):
        """Return the number of elements in the queue."""
        return self._size

    def is_empty(self):
        """Return True if the queue is empty."""
        return self._size == 0

    def first(self): # who is next in queue?
        """Return (but do not remove) the element at the front of the queue."""
        if self.is_empty():
            raise Empty("Queue is empty!")
        return self._head._element # front aligned with head of list

    def dequeue(self):
        """Remove and return the first element of the queue (i.e., FIFO).
        Raise Empty exception if the queue is empty.
        """
        if self.is_empty():
            raise Empty("Queue is empty fam, you cannot do that.")
        answer = self._head._element
        self._head = self._head._next
        self._size -= 1 
        if self.is_empty(): # special case as queue is empty
            self._tail = None # removed head had been the tail
        return answer

    def enqueue(self, e): # new person in the bank queue.
        """Add an element to the back of queue."""
        newest = self._Node(e, None) # node will be new tail node

        if self.is_empty():
            # special case: previously empty
            self._head = newest 
        else:
            # not empty, tail is pointing to newest
            self._tail._next = newest

        # update reference to tail node
        self._tail = newest 
        self._size += 1

In this implementation, we had to accurately maintain the _tail reference.

In terms of performance, the LinkedQueue is similar to the LinkedStack in that all operations run in worst-case constant time, and the space usage is linear in the current number of elements.

Circularly Linked Lists 😯¶

The array approach of ours for circularity was just and abstraction with the usage of modulo arithmetic.

With pointers we can actually make circular Linked Lists. 🥰

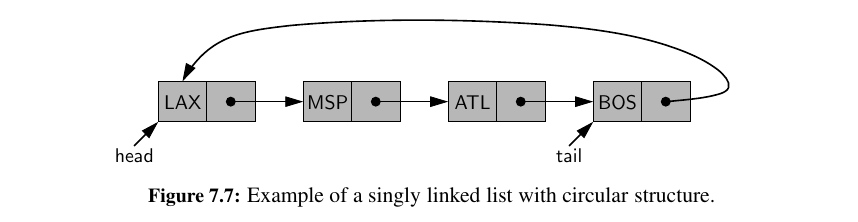
circular_singly_linked_lists — A Circular Structure for a SLL!

A circularly linked list provides a more general model than a standard linked list for data sets that are cyclic, that is, which do not have any particular notion of a beginning and end. Here is a more symmetric illustration to the same Circular Linked List:

circular_linked_lists — A Circular Linked List!

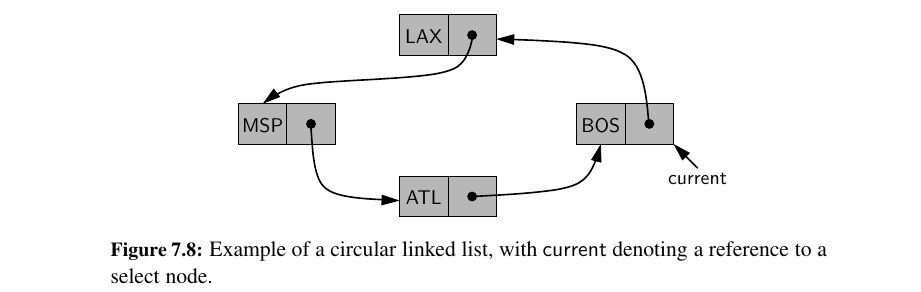
Even though a circularly linked list has no beginning or end, per se, we must maintain a reference to a particular node in order to make use of the list. We use the identifier current to describe such a designated node.

Round-Robin Schedulers¶

This part is just for training.

To motivate the use of a circularly linked list, we consider a round-robin scheduler, which iterates through a collection of elements in a circular fashion and “services” each element by performing a given action on it.

Such a scheduler is used, for example, to fairly allocate a resource that must be shared by a collection of clients.

For instance, round-robin scheduling is often used to allocate slices of CPU time to various applications running concurrently on a computer.

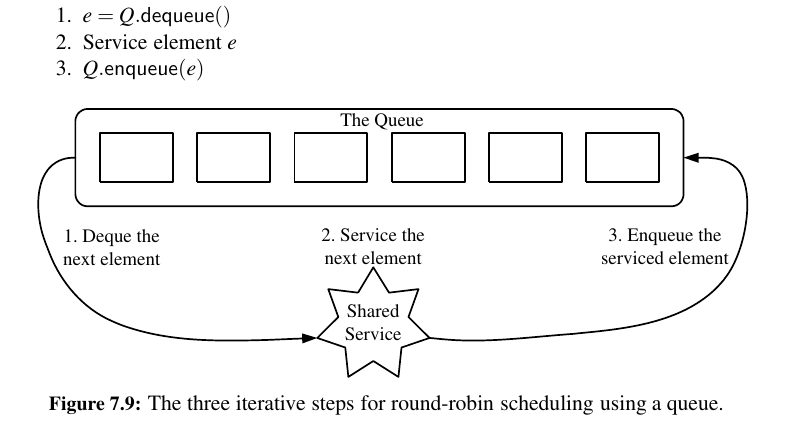
We can do this operation better in the following way:

With a CircularQueue class that supports the entire queue ADT, together with an additional method, rotate(), that moves the first element of the queue to the back (A similar method is supported by the deque class of Python’s collections module - collections.deque).

With this operation, a round-robin schedule can more efficiently be implemented by repeatedly performing the following steps:

Service element Q.front()
Q.rotate()

Implementing a Queue with a Circularly Linked List¶

This is for training as well.

We only need _tail pointer because we know the _head can be found by following the _tail's next reference. We will have a rotate method as we expect.

Here is the code:

circular_queue.py
class Empty(Exception): pass

class CircularQueue:
    """Queue implementation using circularly linked list for storage"""
    class _Node:
        __slots__ = "_element",  "_next" # streamline memory usage

        def __init__(self, element, next):
            self._element = element # reference to user element
            self._next = next # reference to next node

    def __init__(self,):
        self._tail = None # will represent tail of the queue
        self._size = 0 # number of queue elements

    def __len__(self):
        """Return number of elements in the queue"""
        return self._size

    def is_empty(self):
        """Return True if queue is empty."""
        return self._size == 0

    def first(self):
        """Return but do not remove the element at the front of the queue

        Raise Exception if queue is empty"""
        if self.is_empty():
            raise Empty("Queue is empty")
        head = self._tail._next
        return head._element

    def dequeue(self):
        """Remove and return the first element of the queue

        Raise Exception if queue is empty"""
        if self.is_empty():
            raise Empty("Queue is empty")

        # item to be removed
        old_head = self._tail._next

        # removing the only element in the queue
        if self._size == 1: # removing only element
            self._tail = None # queue becomes empty
        else:
            # it has to point to the next element in the queue
            # we kinda breaked the chain by removing reference.
            self._tail._next = old_head._next 
        # decrement size
        self._size -= 1

        return old_head._element

    def enqueue(self, e):
        """Add en element to the back of the queue"""
        newest = self._Node(e, None) # new node
        # if there is no element in the queue
        # initialize circularly
        if self.is_empty():
            # empty and circular
            newest._next = newest
        else:
            newest._next = self._tail._next # new node (latest element) points to head
            self._tail._next = newest # head points to the new node

        self._tail = newest # tail node is now newest
        self._size += 1

    def rotate(self):
        """Rotate front element to the back of the queue"""
        if self._size > 0:
            # basically change where the tail is pointing to
            self._tail = self._tail._next # change tail node to the next one

    def __str__(self):
        """Return a string representation of the circular queue."""
        if self.is_empty():
            return "Empty CircularQueue"

        current = self._tail._next
        elements = [str(current._element)]

        while current._next != self._tail._next:
            current = current._next
            elements.append(str(current._element))

        return ' -> '.join(elements)

Here is the collections.deque rotate method:

from collections import deque

a = deque()

a.append(3)
a.append(4)
a.append(5)

print(a) # dequeue([3,4,5])
a.rotate()
print(a) # dequeue([4,5,3])

Doubly Linked Lists 🏯¶

In a singly linked list, each node maintains a reference to the node that is immediately after it.

We emphasized that we can efficiently insert a node at either end of a singly linked list, and can delete a node at the head of a list, but we are unable to efficiently delete a node at the tail of the list. 😕

More generally, we cannot efficiently delete an arbitrary node from an interior position of the list if only given a reference to that node, because we cannot determine the node that immediately precedes the node to be deleted (yet, that node needs to have its next reference updated).

To provide greater symmetry, we define a linked list in which each node keeps an explicit reference to the node before it and a reference to the node after it.

Such a structure is known as a Doubly Linked List. (DLL) 💕

We continue to use the term next for the reference to the node that follows another, and we introduce the term prev for the reference to the node that precedes it.

Header and Sentinels 🤔¶

In order to avoid some special cases when operating near the boundaries of a doubly linked list, it helps to add special nodes at both ends of the list: a header node at the beginning of the list, and a trailer node at the end of the list.

These “dummy” nodes are known as sentinels (or guards), and they do not store elements of the primary sequence.

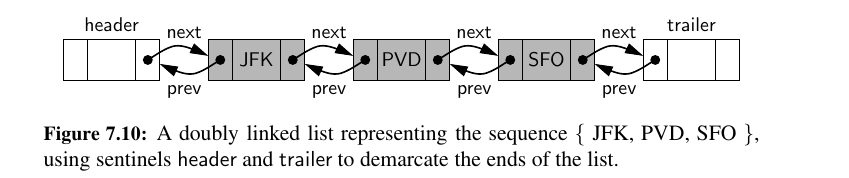
When using sentinel nodes, an empty list is initialized so that the next field of the header points to the trailer, and the prev field of the trailer points to the header; the remaining fields of the sentinels are irrelevant (presumably None, in Python).

Although we could implement a doubly linked list without sentinel nodes (as we did with our singly linked list in Chapter 7), the slight extra space devoted to the sentinels greatly simplifies the logic of our operations.

Most notably, the header and trailer nodes never change—only the nodes between them change.

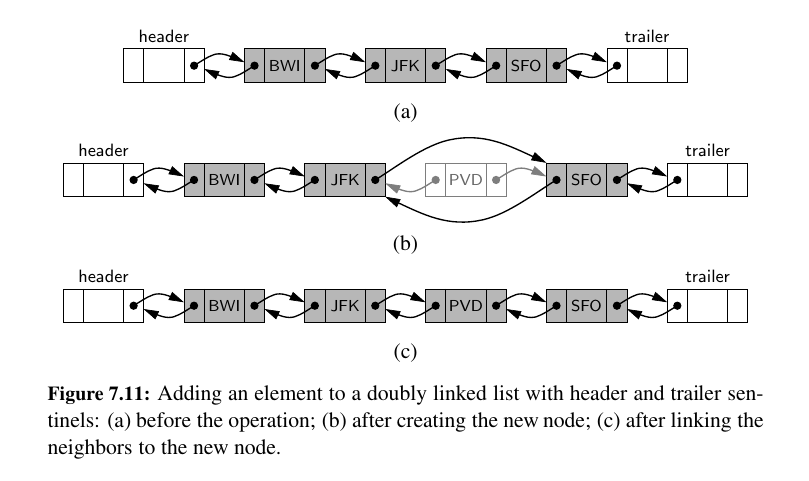
Inserting and Deleting with a Doubly Linked List¶

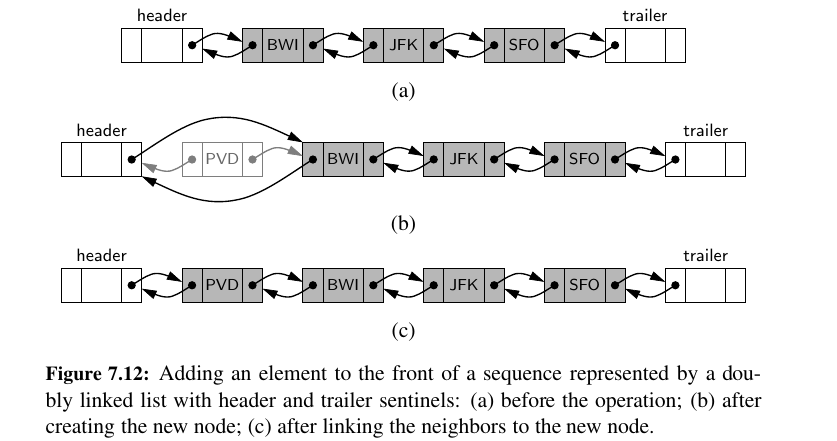
When a new element is inserted at the front of the sequence, we will simply add the new node between the header and the node that is currently after the header.

Here is how you insert to middle'ish position:

adding_to_a_doubly_linked_list — Adding to middleish position

Here is how you insert at front:

The deletion of a node, proceeds in the opposite fashion of an insertion.

The two neighbors of the node to be deleted are linked directly to each other, thereby bypassing the original node. As a result, that node will no longer be considered part of the list and it can be reclaimed by the system.

Here is how you delete from a node:

Basic Implementation of a Doubly Linked List¶

We begin by providing a preliminary implementation of a doubly linked list, in the form of a class named _DoublyLinkedBase.

We intentionally name the class with a leading underscore because we do not intend for it to provide a coherent public interface for general use.

We will see that linked lists can support general insertions and deletions in \(O(1)\) worst-case time, but only if the location of an operation can be succinctly identified.

With array-based sequences, an integer index was a convenient means for describing a position within a sequence.

However, an index is not convenient for linked lists as there is no efficient way to find the jth element; it would seem to require a traversal of a portion of the list.

The constructor instantiates the two sentinel nodes and links them directly to each other. We maintain a _size member and provide public support for __len__ and is_empty so that these behaviors can be directly inherited by the subclasses.

Here is the code:

doubly_linked_base.py
class _DoublyLinkedBase:
    """A base class providing doubly linked list representation"""

    class _Node:
        __slots__ = "_element", "_next", "_prev" # streamline memory usage

        def __init__(self, element, next, prev):
            self._element = element # element of the node
            self._next = next # connect to next node
            self._prev = prev # connect to previous node

    def __init__(self,):
        """Make a new DoublyLinkedList"""
        # These nodes are sentries. They never have elements and 
        # everything happens in between them
        self._header =  self._Node(None, None, None)
        self._trailer =  self._Node(None, None, None)

        # initially no element in the list
        self._header._next = self._trailer
        self._trailer._prev = self._header
        self._size = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def _insert_between (self, e, predecessor, successor):
        """Add an element between two existing nodes and return the new node"""
        # make a new node
        newest = self._Node(e, predecessor, successor)

        # connect to the list
        predecessor._next = newest
        successor._prev = newest

        self._size += 1
        return newest

    def _delete_node (self, node):
        """Delete nonsentinel node from the list and return the nodes element"""

        # find where the the given node in the list 
        predecessor = node._prev 
        successor = node._next

        # make new connections, jumping over the given node
        predecessor._next = successor
        successor._prev = predecessor

        # decrease size
        self._size -=1

        element = node._element # get element

        node._prev = node._next = node._element = None # depracate Node

        return element

The other two methods of our class are the nonpublic utilities, _insert_between and _delete_node.

Implementing a Deque with a Doubly Linked List¶

This part is just for training.

Tip

The double-ended queue (deque) ADT was introduced in Chapter 6.

With an array-based implementation, we achieve all operations in amortized \(O(1)\) time, due to the occasional need to resize the array.

With an implementation based upon a doubly linked list, we can achieve all deque operation in worst-case \(O(1)\) time.

Here is the code:

linked_deque.py
class LinkedDeque(_DoublyLinkedBase):  # note the use of inheritance
    """Double-ended queue implementation based on a doubly linked list."""

    def first(self):
        """Return (but do not remove) the element at the front of the deque.
        Raise Empty exception if the deque is empty.
        """
        if self.is_empty():
            raise Empty("Deque is empty")
        return self._header._next._element  # real item just after header

    def last(self):
        """Return (but do not remove) the element at the back of the deque.
        Raise Empty exception if the deque is empty.
        """
        if self.is_empty():
            raise Empty("Deque is empty")
        return self._trailer._prev._element  # real item just before trailer

    def insert_first(self, e):
        """Add an element to the front of the deque."""
        self._insert_between(e, self._header, self._header._next)  # after header

    def insert_last(self, e):
        """Add an element to the back of the deque."""
        self._insert_between(e, self._trailer._prev, self._trailer)  # before trailer

    def delete_first(self):
        """Remove and return the element from the front of the deque.
        Raise Empty exception if the deque is empty.
        """
        if self.is_empty():
            raise Empty("Deque is empty")
        return self._delete_node(self._header._next)  # use inherited method

    def delete_last(self):
        """Remove and return the element from the back of the deque.
        Raise Empty exception if the deque is empty.
        """
        if self.is_empty():
            raise Empty("Deque is empty")
        return self._delete_node(self._trailer._prev)  # use inherited method

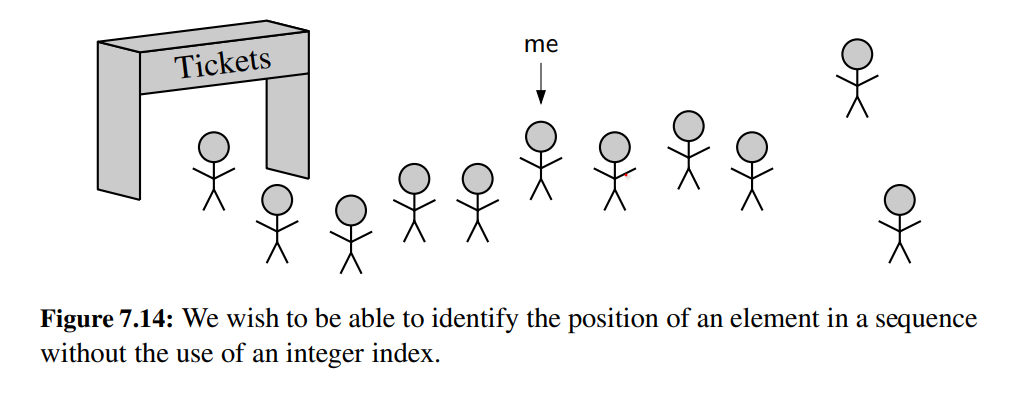
The Positional List ADT¶

Warning

I have not bumped into a Data Structure like this one in my work, so far. This might be a little too much for diving deep and might be not necessary for beginners.

The abstract data types that we have considered thus far, namely stacks, queues, and double-ended queues, only allow update operations that occur at one end of a sequence or the other.

Although we motivated the FIFO semantics of a queue as a model for customers who are waiting to speak with a customer service representative, or fans who are waiting in line to buy tickets to a show, the queue ADT is too limiting.

What if a waiting customer decides to hang up before reaching the front of the customer service queue?

Or what if someone who is waiting in line to buy tickets allows a friend to “cut” into line at that position?

We would like to design an abstract data type that provides a user a way to refer to elements anywhere in a sequence, and to perform arbitrary insertions and deletions.

identify_one — Identify posisition without an index ?

A Word Processor¶

As another example, a text document can be viewed as a long sequence of characters.

A word processor uses the abstraction of a cursor to describe a position within the document without explicit use of an integer index, allowing operations such as “delete the character at the cursor” or “insert a new character just after the cursor.”

Furthermore, we may be able to refer to an inherent position within a document, such as the beginning of a particular section, without relying on a character index (or even a section number) that may change as the document evolves.

A Node Reference as a Position?¶

One of the great benefits of a linked list structure is that it is possible to perform O(1)-time insertions and deletions at arbitrary positions of the list, as long as we are given a reference to a relevant node of the list.

It is therefore very tempting to develop an ADT in which a node reference serves as the mechanism for describing a position. In fact, our _DoublyLinkedBase class has methods insert between and delete node that accept node references as parameters.

However, such direct use of nodes would violate the object-oriented design principles of abstraction and encapsulation.

There are several reasons to prefer that we encapsulate the nodes of a linked list, for both our sake and for the benefit of users of our abstraction.

• It will be simpler for users of our data structure if they are not bothered with unnecessary details of our implementation, such as low-level manipulation of nodes, or our reliance on the use of sentinel nodes.

• We can provide a more robust data structure if we do not permit users to directly access or manipulate the nodes. In that way, we ensure that users cannot invalidate the consistency of a list by mismanaging the linking of nodes.

• By better encapsulating the internal details of our implementation, we have greater flexibility to redesign the data structure and improve its performance. In fact, with a well-designed abstraction, we can provide a notion of a non-numeric position, even if using an array-based sequence.

For these reasons, instead of relying directly on nodes, we introduce an independent position abstraction to denote the location of an element within a list, and then a complete positional list ADT that can encapsulate a doubly linked list.

The Positional List Abstract Data Type¶

To provide for a general abstraction of a sequence of elements with the ability to identify the location of an element, we define a positional list ADT as well as a simpler position abstract data type to describe a location within a list.

A position acts as a marker or token within the broader positional list.

...